وتتوزع الأقمار الصناعية في مدار يعرف بمدار كلارك وهو عبارة عن طوق يحيط بالكرة الأرضية فوق خط الإستواء مباشرة موازيا له ويبعد عنه وعن سطح الأرض بمسافة 36 ألف كيلو مترا
==========================
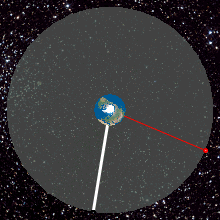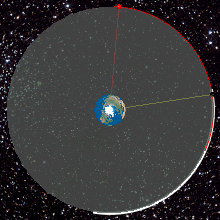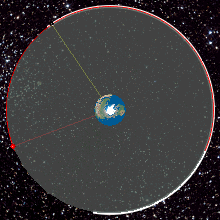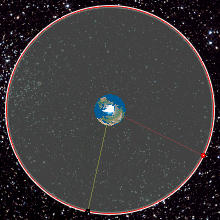
المدار الجغرافي الثابت (مسقط رأسي) بالنسبة لمشاهد على الأرض المتحركة كل قمر صناعي يبدو ثابت في السماء في المكان الخاص به
المدار الجغرافي الثابت هو مدار دائري على ارتفاع 35,786 كيلومتر (22,236 ميل) فوق خط الاستواء وفي نفس اتجاه دوران الأرض. أي جسم في هذا المدار يكون له فترة مدارية تساوي الوقت اللازم ليتم كوكب الأرض دورة كاملة حول نفسه (يوم فلكي) وبالتالي يبدو كأنه في موقع ثابت لا يتحرك بالنسبة لمشاهد على الأرض. أقمار الاتصالات وأقمار الأرصاد الجوية غالباً يتم وضعها في المدار الجغرافي الثابت وذلك حتى لا تضطر الهوائيات الأرضية التي تتصل بها أن تتحرك معها لمتابعتها، بل يتم توجيهها لنقطة ثابتة في السماء التي يوجد بها القمر المطلوب. المدار الجغرافي الثابت هو أحد أنواع المدارات المتزامنة. فكرة الأقمار الصناعية في المدارات المتزامنة بغرض الاتصالات تم نشرها لأول مرة عام 1928 (ولكنها لم تنتشر بشكل كبير حينها) بواسطة هرمان بوتوكنيك. فكرة المدار الجغرافي الثابت انتشرت على نطاق واسع عام 1945 في مقال بعنوان "المبدلات خارج كوكب الأرض - هل تستطيع المحطات الصاروخية توفير تغطية راديو عالمية؟" من تأليف كاتب الخيال العلمي البريطانيآرثر سي كلارك ونشرت في مجلة "عالم اللاسلكي Wireless World". المدار الذي وصفه كلارك على أنه يمكن استخدامه لأقمار التغطية الإذاعية والاتصالات يسمى أحياناً مدار كلارك.

المدار الجغرافي الثابت (مسقط جانبي)
كذلك يوجد حزام كلارك والذي هو جزء من الفضاء على ارتفاع 35,786 كيلومتر (حوالي 22,000 ميل) فوق سطح البحر في مستوى خط الاستواء، حيث توجد المدارات شبيهة المدارات الجغرافية الثابتة وهو بطول حوالي 265,000 كيلومتر (165,000 ميل).
التطبيقات العملية
معظم أقمار الاتصالات والبث توجد في المدار الجغرافي الثابت. مدار النقل للمدار الجغرافي الثابت هو مدار يستخدم لنقل القمر الصناعي من مدار أرضي منخفض إلى مدار جغرافي ثابت. بعض أقمار البث التلفيزيون الروسية استخدمت مدارات مولنيا وتوندرا ذات الشكل البيضاوي بسبب وجود المتلقي في دوائر عرض عالية. أول قمر صناعي وضع في المدار الجغرافي الثابت كان القمر سينكوم-3 (Syncom-3), وتم إطلاقه على صاروخ من نوع دلتا-دي (Delta-D) في عام 1964. شبكات عالمية من أقمار الأرصاد الجوية العاملة تستخدم لالتقاط صور مرئية وصور بالأشعة تحت الحمراء لسطح الأرض والغلاف الجوي. وهذه الأنظمة تتضمن:
نظام جويس التابع للولايات المتحدة.
نظام ميتيوسات أطلق بواسطة وكالة الفضاء الأوروبية ويتم تشغليه بواسطة المنظمة الأوربية للأرصاد الجوية.
نظام ميتسات (MTSAT) الياباني.
نظام إنسات (INSAT) الهندي.
يوجد فرضيات نظرية لأقمار صناعية تعمل بما يسمى الشراع الشمسي لتعديل المدار (يطلق عليها بالإنجليزية Statite)، هذه الأقمار يمكنها نظرياً الحفاظ على موقعها في مدار ثابت جغرافياً حتى مع تغير الارتفاع وميل المدار عن المدار الجغرافي الثابت المعتاد عليه فوق خط الاستواء.
الاستقرار في المدار
المدار الجغرافي الثابت يمكن تحقيقه فقط عند ارتفاع قريب جداً من 35,786 كيلومتر (22,236 ميل)، وفوق خط الأستواء تماماً. وهذا يساوى سرعة مدارية تساوي 3.07 كيلومتر/ثانية (1.91 ميل/ثانية) وفترة مدارية تساوي 1,436 دقيقة، والتي تساوي بالضبط يوم فلكي واحد تقريباً أو 23.934461223 ساعة. وهذا يضمن تزامن القمر الصناعي مع دوران الأرض حول نفسها وثباته فوق نقطة واحدة من الأرض دائماً. جميع أقمار الثبات الجغرافي يجب أن تتواجد في هذه الحلقة. ويسبب اتحاد العوامل الآتية: الجاذبية القمرية والجاذبية الشمسية وتفلطح الأرض عند قطبيها؛ يسبب هذا المزيج ترنح في المستوى المدارى لأي جسم في مدار الثبات الجغرافي بدورة تساوي 53 سنة تقريباً ومعدل انحدار مبدأي يساوي 0.85 درجة كل عام ويتم أقصى انحدار يساوي 15 درجة كل 26.5 سنة. ولتصحيح هذا الاضطراب في المدار يلزم استخدام مناورات تثبيت الموقع في المدار وتقدر بتغير في السرعة يساوي 50 متر/ثانية كل عام. تأثير آخر يجب أخذه في الاعتبار ألا وهو الانجراف على خطوط الطول وسببه اللاتماثل في الكرة الأرضية - خط الاستواء بيضاوي الشكل قليلاً. يوجد نقطتي توازن مستقرتين عند خطي طول 75.3° شرق و104.7° غرب، ونقطتي توازن غير مستقرتين عند خطي طول 165.3° شرق و14.7° غرب. أي جسم في مدار الثبات الجغرافي بين نقطتي توازن سيتأثر بعجلة تسارع صغيرة (بدون أي مؤثر خارجي غير قوى الجاذبية) نحو نقطة التوازن المستقر مما يتسبب بتغير مستمر في خط الطول وتصحيح هذا التأثير يلزم مناورات للتحكم في المدار بتغيير في السرعة المدارية بحد أقصى 2 متر/ثانية كل عام اعتماداً على خط الطول المطلوب. وتؤثر أيضاً كلاً من الرياح الشمسية والضغط الإشعاعي بقوى صغيرة على الأقمار الصناعية مما يؤدي لتغييرات بسيطة في مداراتها. وفي غياب أي مهمات صيانة من الأرض واستهلاك وقود الدفع (المستخدم في صواريخ التحكم) لتثبيت مكان القمر يحدد العمر الأفتراضي للقمر الصناعي لأنه في حالة الاستهلاك الكامل للوقود سينحرف القمر الصناعي عن مكانه ولا يوجد وسيلة لتصحيح الخطأ فيصبح - في أغلب الأحوال - بلا فائدة حتى ولو كانت المعدات في حالة جيدة.
الاتصالات
الأقمار الصناعية في
مدار الثبات الجغرافي بعيدة جداً لدرجة تسبب تأخر ملحوظ في الاتصالات - يقدر بحوالي ربع ثانية خلال رحلة من محطة إرسال أرضية إلى القمر الصناعي ورجوعاً إلى المحطة الأرضية وحوالي نصف ثانية عند نقل الإشارة من محطة أرضية إلى أخرى أرضية ثم عودتها للأولى مجدداً. على سبيل المثال؛ بالنسبة للمحطات الأرضية بين دائرتي عرض (رمزها) +45° و-45° وعلى نفس خط طول القمر الصناعي، الوقت اللازم لتسافر الإشارة من محطة أرضية إلى القمر الصناعي ثم رجوعاً إلى المحطة الأرضية يمكن حسابه باستخدام قاعدة جيب التمام على افتراض معرفة الآتي: نصف قطر
مدار الثبات الجغرافى ورمزه هنا r (مستنتجة لاحقاً) ونصف قطر الأرض ورمزه هنا R، وسرعة الضوء ورمزها هنا c (التي هي سرعة الموجات الكهرومغناطيسية والتي تندرج تحتها إشارة الاتصالات).
2 R 2 + r 2 − 2 R r cos φ c ≈ 253 m s {\displaystyle 2{\frac {\sqrt {R^{2}+r^{2}-2Rr\cos \varphi }}{c}}\approx 253\,\mathrm {ms} } {\displaystyle 2{\frac {\sqrt {R^{2}+r^{2}-2Rr\cos \varphi }}{c}}\approx 253\,\mathrm {ms} }
لاحظ هنا أن نصف قطر المدار r هنا هو المسافة بين مركز الأرض حتى المدار وليس ارتفاع المدار فوق سطح الأرض. هذا التأخير يسبب مشاكل في التطبيقات الحساسة للتأخير مثل الأتصالات الصوتية وألعاب الكمبيوتر المباشرة على الإنترنت.
الأقمار الصناعية في مدارات الثبات الجغرافي تكون فوق خط الاستواء مباشرةً وتدنو لأسفل في السماء كلما اتجهنا شمالاً أو جنوباً من خط الأستواء. وفي دوائر العرض البعيدة (قرب قطبي الأرض)، تبدو الأقمار الصناعية منخفضة جداً وبالتالي تصبح الاتصالات صعبة وربما مستحيلة بسبب بعض العوامل مثل: الانحراف الأشعة عبر الغلاف الجوي، الانبعاثات الحرارية للأرض، الموانع المادية عبر خط النظر (الجبال والمباني المرتفعة) وانعكاس الإشارات عن سطح الأرض أو المباني، وفي دوائر العرض الأكبر من 81° تختفي الأقمار الصناعية في مدارات الثبات الجغرافي تحت خط الأفق وبالتالي لا تُرى نهائياً.
تقسيم المدار
جميع الأقمار الصناعية في
مدار الثبات الجغرافي يجب أن تتواجد في حلقة واحدة فوق خط الاستواء تماماً، وضرورة الفصل بين هذه الأقمار لتجنب تداخل الموجات العاملة تعني أنه يوجد عدد محدود من المواقع المتاحة في المدار، وبالتالي عدد محدود من الأقمار يمكن تشغيلها في
مدار الثبات الجغرافي. هذه القيود أدت إلى نشأة صراعات بين الدول المختلفة الراغبة في امتلاك أقمار صناعية في
مدار الثبات الجغرافي في نفس خط الطول وبنفس الترددات (الدول التي توجد على دوائر عرض مختلفة ولكن نفس خط الطول). هذه النزاعات يتم حلها عبر آلية التقسيم الخاصة بالاتحاد الدولي للاتصالات. في إعلان بوجوتا الصادر عام 1976، أعلنت ثماني دول واقعة على خط الاستواء سيادتها على مدارات الثبات الجغرافي الواقعة فوق أراضيها على اعتبارها ثروات طبيعية ولكن الإعلان لم يلق اعتراف دولي.
ويوجد حالياً معاهدات دولية لتقسيم الأماكن في المدار وتقسيم الترددات كذلك.
بالنسبة للأقمار الصناعية التي خرجت من الخدمة في نهاية فترة العمر المحددة لها (بمعنى انتهاء وقود الدفع الذي يصحح مسارها) إما أن يتواصل استخدامها في مداراتها الجديدة المائلة أو يتم دفعها بعيداً عن المدار الجغرافي الثابت إلى
مدار أعلى منه يطلق عليه "المقبرة" أو "مدار المهملات".
استنتاج ارتفاع المدار الجغرافي الثابت
في أي
مدار دائري القوة المضادة للقوة الطاردة المركزية المطلوبة للحفاظ على المدار (Fc) تنتج عن قوة الجاذبية المؤثرة على القمر (Fg). لحساب ارتفاع المدار الجغرافي الثابت نبدأ بالمعادلة التالية:
F c = F g {\displaystyle \mathbf {F} _{\text{c}}=\mathbf {F} _{\text{g}}} {\displaystyle \mathbf {F} _{\text{c}}=\mathbf {F} _{\text{g}}}
باستخدام قانون نيوتن الثاني للحركة، يمكن استبدال القوى F بكتلة الجسم m مضروبة في عجلة التسارع التي يشعر بها الجسم نتيجة لهذه القوة:
m a c = m g {\displaystyle m\mathbf {a} _{\text{c}}=m\mathbf {g} } {\displaystyle m\mathbf {a} _{\text{c}}=m\mathbf {g} }
نلاحظ أن كتلة القمر الصناعي m تظهر في كلا الطرفين -
مدار الثبات الجغرافي لا يعتمد على كتلة القمر الصناعي.
لذلك يمكن تبسيط معادلة حساب الارتفاع إلى حساب النقطة التي يتساوى فيها مقدار العجلة الناتجة عن القوة المضادة للطاردة المركزية اللازمة للحركة المدارية بعجلة الجاذبية المؤثرة من الأرض على القمر الصناعي. مقدار العجلة الناتجة عن القوة المضادة للطاردة المركزية عبارة عن:
| a c | = ω 2 r {\displaystyle |\mathbf {a} _{\text{c}}|=\omega ^{2}r} {\displaystyle |\mathbf {a} _{\text{c}}|=\omega ^{2}r}
حيث ω هي السرعة الزاوية، وr هي نصف قطر المدار مقاساً من مركز الثقل للكرة الأرضية. مقدار عجلة الجاذبية عبارة عن:
| g | = G M r 2 {\displaystyle |\mathbf {g} |={\frac {GM}{r^{2}}}} {\displaystyle |\mathbf {g} |={\frac {GM}{r^{2}}}}
حيث M هي كتلة الكرة الأرضية والتي تساوي 5.9736 × 1024 كيلوجرام، وG هي ثابت الجذب العام والذي يساوي 6.67428 ± 0.00067 × 10−11 م3 كجم−1 ث−2 وبمساواة العجلتين نستنتج أن:
r 3 = G M ω 2 → r = G M ω 2 3 {\displaystyle r^{3}={\frac {GM}{\omega ^{2}}}\to r={\sqrt[{3}]{\frac {GM}{\omega ^{2}}}}} {\displaystyle r^{3}={\frac {GM}{\omega ^{2}}}\to r={\sqrt[{3}]{\frac {GM}{\omega ^{2}}}}}
حاصل الضرب التالي GM معروف بدقة أكبر من أي من العاملين بمفرده ويطلق عليه ثابت الجذب الأرض-مركزي μ = 398,600.4418 ± 0.0008 km3 s−2:
r = μ ω 2 3 {\displaystyle r={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}} {\displaystyle r={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}}
السرعة الزاوية ω يمكن استنتاجها بقسمة الزاوية المقطوعة خلال دورة واحدة (360° = 2π rad) على الفترة المدارية (الوقت المطلوب لقطع دورة واحدة كاملة). في حالة المدار الجغرافي الثابت؛ الفترة المدارية هي يوم فلكي واحد أو 86,164.09054 ثانية.
وينتج عن هذا التالي:
ω ≈ 2 π r a d 86 164 s ≈ 7.2921 × 10 − 5 r a d / s {\displaystyle \omega \approx {\frac {2\mathrm {\pi } ~\mathrm {rad} }{86\,164~\mathrm {s} }}\approx 7.2921\times 10^{-5}~\mathrm {rad} /\mathrm {s} } {\displaystyle \omega \approx {\frac {2\mathrm {\pi } ~\mathrm {rad} }{86\,164~\mathrm {s} }}\approx 7.2921\times 10^{-5}~\mathrm {rad} /\mathrm {s} }
نصف قطر المدار الناتج يساوي 42,164 كيلومتر (26,199 ميل). وبطرح نصف قطر الأرض عند خط الاستواء والذي يساوي 6378 كيلومتر (3,963 ميل)، يتبقى لنا ارتفاع 35,786 كيلومتر (22,236 ميل). أما السرعة المدارية (السرعة التي يتحرك بها القمر الصناعي خلال الفضاء) فيتم حسابها بضرب السرعة الزاوية في نصف قطر المدار:
v = ω r ≈ 3.0746 k m / s ≈ 11 068 k m / h ≈ 6877.8 m p h . {\displaystyle v=\omega r\approx 3.0746~\mathrm {km} /\mathrm {s} \approx 11\,068~\mathrm {km} /\mathrm {h} \approx 6877.8~\mathrm {mph} {\text{.}}} {\displaystyle v=\omega r\approx 3.0746~\mathrm {km} /\mathrm {s} \approx 11\,068~\mathrm {km} /\mathrm {h} \approx 6877.8~\mathrm {mph} {\text{.}}}
أي أن السرعة المدارية تساوي 3.0746 كم/ث أو 11,068 كم/س أو 6877.8 ميل/س.
 التعليمات الإدارية
التعليمات الإدارية « آخـــر الــمــواضــيــع »
« آخـــر الــمــواضــيــع »


